Class 10 Maths Chapter 1 Real Number Solution
प्रश्नावली 1.1 ( Excercise 1.1 ) [ यूक्लिड विभाजन Remove Syllabus in Class 10th Maths]
प्रश्नावली 1.2
निम्नलिखित संख्याओं को अभाज्य गुणनखंडों के गुणनफल के रूप में व्यक्त कीजिए :
(i) 140 , (ii) 156 (iii) 3825 (iv) 5005 (v) 7429
Solve :
140 = 2×2×5×7= 22 × 51× 71
156 = 2×2×3×13 = 22 × 31× 131
3825 = 3×3 ×5×5×17 = 32 × 52×171
5005 = 5×7×11×13 = 51 × 71 × 111 × 131
7429 = 17×19×23 =171 × 19 1 × 231
प्रश्न 2 पूर्णांकों के निम्नलिखित युग्मों के HCF और LCM ज्ञात कीजिए तथा इसकी जाँच कीजिए कि दो संख्याओं का गुणनफल = HCF × LCM
(i) 26 और 91 (ii) 510 और 92 (iii) 336 और 54
Solve:
(i) 26 और 91
26 = 2 × 13
91 = 7 × 13
HCF =13
LCM = 2 × 7 ×13 = 182
(ii) 510 और 92
510 = 2 × 3 × 5 ×17
92 = 2 × 2 × 23
HCF = 2
LCM = 2× 2× 3× 5× 17× 23 = 23460
अब HCF (510, 92) × LCM (510, 92) = 2 × 23460 = 46920
(iii) 336 और 54
Solve :
336 = 2 × 2 × 2 × 2 × 3 × 7
54 = 2 × 3 × 3 × 3
HCF = 2 × 3 = 6
LCM = 2 × 2 × 2 × 2 × 3 × 3 × 3 × 7 = 3024
अब HCF (336, 54) × LCM (336, 54) = 6 × 3024 = 18144
एवं 336 × 54 = 18144
Read more
Class 10th NCERT All Subject Syllabus
Cbse Class 10th maths Syllabus
Social Science chapter 1 Solution
प्रश्न 3 अभाज्य गुणनखंड विधि द्वारा निम्नलिखित पूर्णांकों के HCF और LCM ज्ञात कीजिए :
(i) 12, 15 और 21 (ii) 17, 23 और 29 (iii) 8, 9 और 25
Solve :
(i) 12, 15 और 21
12 = 2 × 2 × 3
15 = 3 × 5
21 = 3 × 7
HCF = 3
LCM = 2 × 2 × 3 × 5 × 7 = 420
अत: अभीष्ट HCF= 3 एवं LCM = 420
(ii) 17, 23 और 29
17 = 1 × 17
23 = 1× 23
29 = 1×29
HCF = 1
LCM = 17 × 23 × 29 = 11339
(iii) 8, 9 और 25
8 = 1× 2 × 2 × 2
9 = 1 × 3 × 3
25 = 1 × 5 × 5
HCF = 1
LCM = 2 × 2 × 2 × 3 × 3 × 5 × 5 = 1800
अत: अभीष्ट HCF = 1 एवं LCM = 1800
(iv) 6 = 2 × 3
72 = 2 × 2 × 2 × 3 × 3
120 = 2 × 2 × 2 × 3 × 5
HCF = 2× 3 = 6
LCM = 2 × 2 × 2 × 3 × 3 × 5 = 360
अत:, अभीष्ट HCF = 6 एवं LCM = 360
प्रश्न 4 : HCF (306, 657) = 9 दिया है। LCM (306, 657) ज्ञात कीजिए ।
Solve : LCM (306, 657) × HCF (306, 657) = 306 × 657
[चूंकि HCF (306, 657) = 9 (दिया है) ]
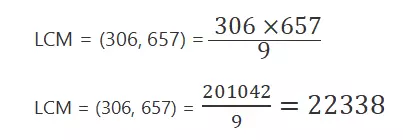
अत:, अभीष्ट LCM (306, 657) = 22338
प्रश्न 5. जाँच कीजिए कि क्या किसी प्राकृत संख्या n के लिए, संख्या 6n अंक 0 पर समाप्त हो सकती है ।
Solve : 6n का अभाज्य गुणनखण्ड = (2× 3)n
जबकि कोई प्राकृत संख्या जो शून्य पर समाप्त होती है उसके अभाज्य गुणनखंड (2× 5)n के रूप का होता है ।
अत: 6n शून्य पर समाप्त नहीं होगी ।
प्रश्न 6. व्याख्या कीजिए कि 7×11×13 +13 और 7× 6 × 5 × 4 × 3 × 2 × 1 + 5 भाज्य संख्याएँ क्यों हैं ।
Solve : माना X = 7× 11 × 13 + 13
= 13 ( 7 × 11 + 1 )
= 13 ( 77 + 1)
= 13 × 78
अत: यह एक भाज्य संख्या है क्योंकि इसके अभाज्य गुणनखंड में 1 को छोड़कर अन्य दो गुणनखंड हैं ।
इसी प्रकार,
माना
Y = 7 × 6 × 5 × 4 × 3 × 2 × 1 + 5
= 5 ( 7 × 6 × 4 × 3 × 2 × 1 + 1)
= 5 × ( 1008 + 1)
= 5 × 1009
अत: यह भी एक भाज्य संख्या है क्योंकि इसके भी अभाज्य गुणनखंड में 1 को छोड़कर अन्य दो गुणनखंड हैं ।
प्रश्न 7. किसी खेल के मैदान के चारों ओर एक वृत्ताकार पथ है । इस मैदान का एक चक्कर लगाने में सोनिया को 18 मिनट लगते हैं, जबकि इसी मैदान का एक चक्कर लगाने में रवि को 12 मिनट लगते हैं । मान लीजिए वे दोनों एक ही स्थान और एक ही समय पर चलना प्रारंभ करके एक ही दिशा में चलते हैं । कितने समय बाद वे पुन: प्रारंभिक स्थान पर मिलेंगे ?
Solve :
एक चक्कर लगाने में सोनिया को 18 मिनट लगते हैं ।
रवि एक चक्कर में 12 लगाता है ।
वे दोनों एक ही स्थान पर LCM ( 18, 12) मिनट के बाद मिलेंगे ।
अत:
18 = 2 × 3 × 3 =
12 = 2 × 2 × 3
HCF = 2 × 3 = 6
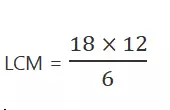
= 36 मिनट ।
प्रश्नावली 1.3 Solutions





